Variables, Types, and Operations
Last updated on 2024-05-23 | Edit this page
Download Chapter notebook (ipynb)
Mandatory Lesson Feedback Survey
Overview
Questions
- What are I/O operations?
- What do variables do?
- Why types and scopes of variables are important?
- What types of operations are used?
Objectives
- Understanding the output and input operations
- Build concepts of different types of variables
- Learning about type conversions and scope
- Understanding mathematical and logical operations
In programming, we process data and produce outputs. When data is being processed, it is stored in a memory, so that it is readily available, and can therefore be subject to the processes we want to apply.
Throughout this section, we will discuss how to handle data in Python. We start by displaying data on the screen, and see how to receive input from a user. We then use these techniques to perform different mathematical and logical operations. This chapter introduces the fundamental principles that we employ every time we code in Python. On that account, make sure you understand everything before moving on.
I/O Operations
In computer science, input or output operations refer to the communication between an information processing system such as a computer, and the outside world, which may be a user or another computer. Such communications are more commonly known as I/O operations. In general, the outside world — especially in the context of this course, may be loosely defined as anything that falls outside of the coding environment.
REMEMBER
Only what we define within the environment and what we store in the memory is directly controlled by our application. We may access or take control over other environments through certain mediums; however, such interactions are classified as I/O operations. An example of this is interacting with a file on our computer, which we discuss in the topic of Strings. Whilst we have complete control over a file while working on it (e.g. reading from it or writing to it), the access to the file and the transmission of data is in fact controlled and managed not by the programming environment but by the operating system of the computer.
In programming, I/O operations include, but are not limited to:
displaying the results of a calculation
require the user to enter a value
writing or reading data to and from a file or a database
downloading data from the Internet
operating a hardware (e.g. a robot)
Advanced Topic
If you are interested in learning more about I/O systems and how they are handled at operating system level, you might benefit from chapter 13 of Operating Systems Concepts, 10th ed. by Abraham Silberschatz, Greg Gagne, and Peter Galvin.
I/O Operations in Python
In this section, we learn about two fundamental methods of I/O operations in Python. We will be using these methods throughout the course, so it is essential that you feel comfortable with them and the way they work before moving on.
Producing an output
The term output in reference to an application typically
refers to data that has either been generated or manipulated by that
application.
For example; we have two number and we would like to calculate their
sum. The action of calculating the sum is itself a mathematical operation (discussed in the
coming section). The result of our calculation is called an
output. Once we obtain the result, we might want to save it
in a file or display it on the screen, in which case we will be
performing an I/O operation.
The simplest and most frequently used method for generating an output in almost every modern programming language is to display something on the screen. We recommend using JupyterLab notebooks to run our scripts and the typical method to produce an output is to display it in cell below the code.To do this, we will call a dedicated built-in function named print().
REMEMBER
In programming, a function is essentially an isolated piece
of code. It usually to takes some inputs, does something to or
with them, and produces an output. The pair of (typically
round) parenthesis that follow a function are there to provide the
function with the input arguments it needs when we
call it, so that it can do what it is supposed to do using our
data. We will explore functions in more details in Lesson 4 Functions.
The print() function can take several inputs and performs different tasks. Its primary objective, however, is to take some values as input and display them on the screen. Here is how it works:
Suppose we want to display some text in the terminal. To do so, we write:
print('Hello world!')in a cell of our notebook (or, if not using a notebook, an editor or IDE) and save the notebook in a file. This is now a fully functioning Python programme that we can run using the Python interpreter.
If you are using an Integrated Development Environment (IDE) —
e.g. Visual Studio Code, you have to save the code in a file with
extension .py and may then execute your code using the
internal tools provided by that IDE. The specifics of how you do so
depend on the IDE that you are using.
.py Python scripts can also be executed manually. To do so,
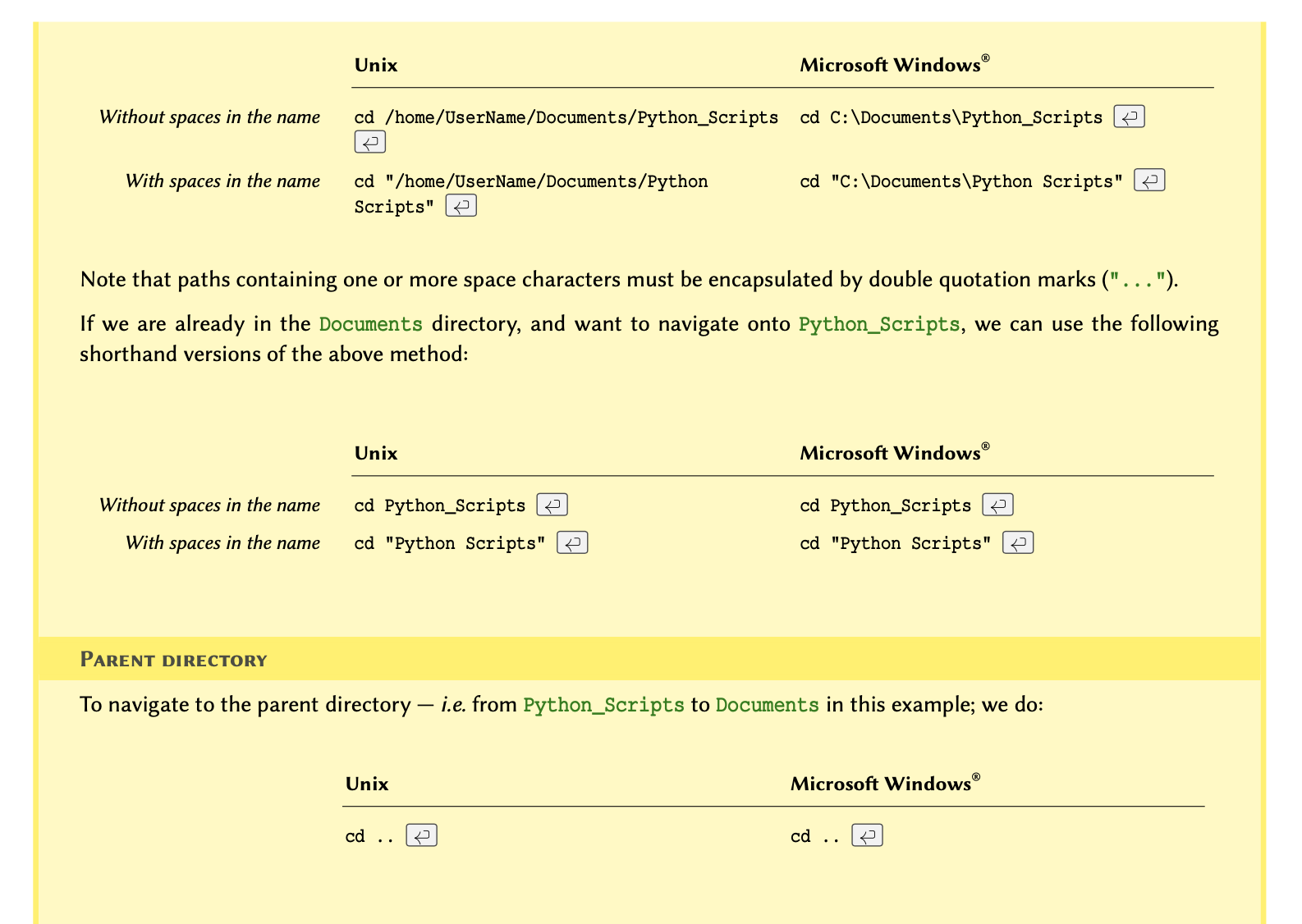
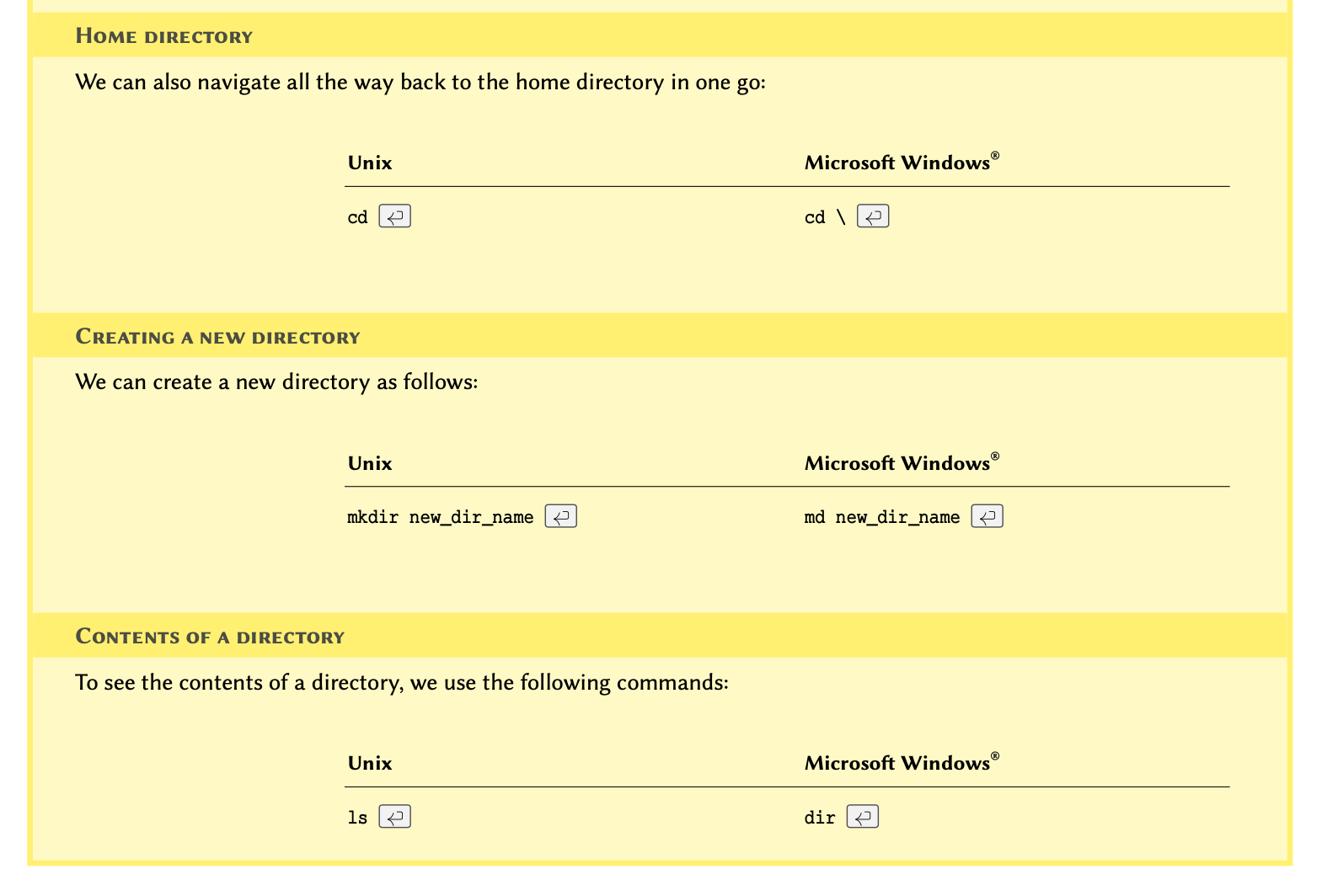
we open the terminal in MacOS or Linux or the command prompt (CMD) in
Windows and navigate to the directory where we saved the script.
NOTE
If you don’t know how to navigate in the terminal, see the example in section How to use terminal environment? at the end of this chapter.
Once in the correct directory, we run a script called
script_a.py by typing python3 script_a.py in
our terminal as follows:
OUTPUT
Hello world!
This will call the Python 3 interpreter to execute the code we wrote in
script_a.py. Once executed, which in this case should be
instantaneously, we should see the output.
In a JupyterLab notebook we can press the keyboard shortcut ‘shift-enter’ to execute the code in a cell. The output will be displayed below the code cell.
Congratulations you have now successfully written and executed your first programme in Python.
REMEMBER
We know print() is a function because it ends with a pair of parenthesis, and it is written entirely in lowercase characters PEP-8: Function Names. Some IDEs change color when they encounter built-in functions in the code so that we won’t accidentally overwrite them. We shall discuss functions in more details in Lesson 4 Functions.
We can pass more than a single value to the print() function, provided that they are separated with a comma. For instance, if we write the code below and run the script, the results would be as shown in output.
OUTPUT
Hello JohnNotice that there is a space between ‘Hello’ and ‘John’ even though we did not include a space in our text. This is the default behaviour of the print() function when it receives more than a single value (argument).
This default behaviour may be changed:
OUTPUT
HelloJohnOUTPUT
Hello--JohnOUTPUT
Jane.21.London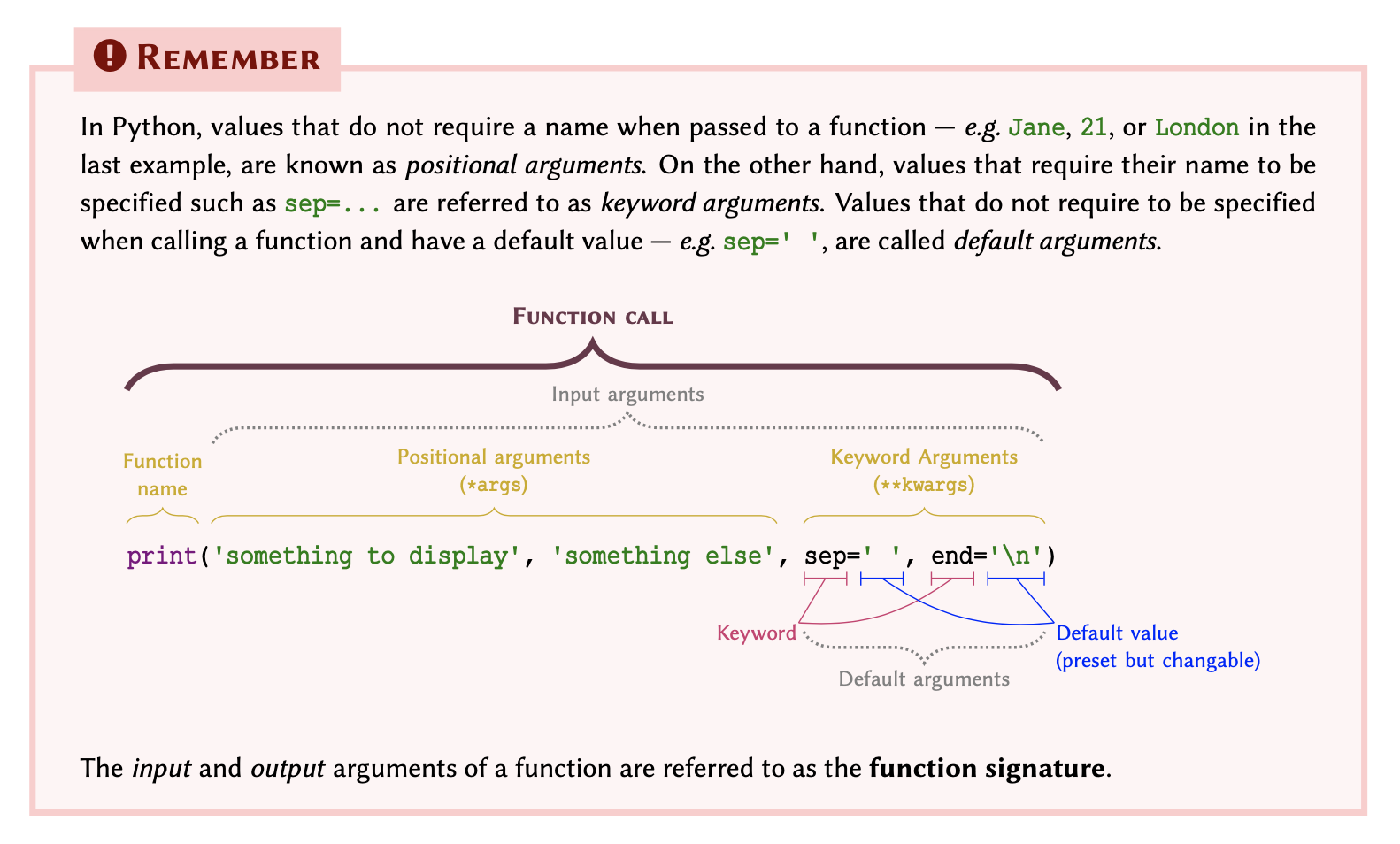
Receiving an input
Inputs are I/O operations that involve receiving some data from the outside world. This might include reading the contents of a file, downloading something from the Internet, or asking the user to enter a value.
The simplest way to acquire an input is to ask the user to enter a value in the terminal. To do so, we use a dedicated built-in function called input().
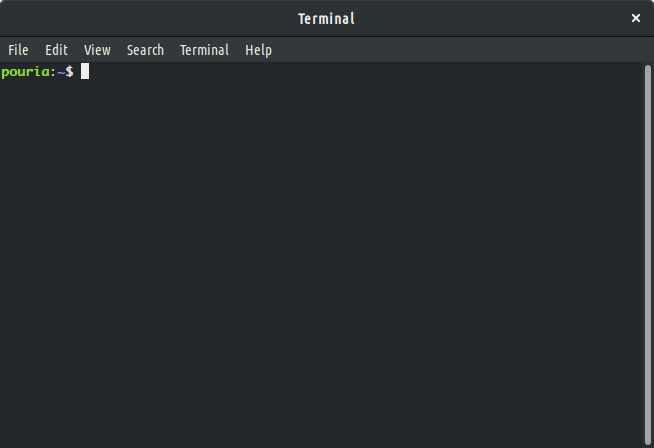
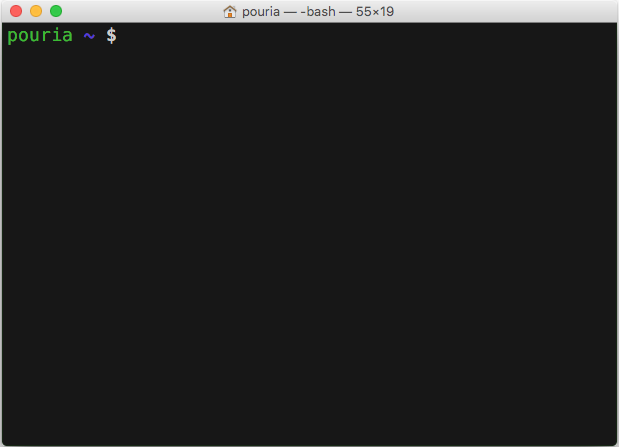
The function takes a single argument called
prompt. Prompt is the text displayed in the terminal to ask
the user for an input. Figure Terminal window on
a Linux computer and Terminal window on a
Mac, illustrates a screen shot of my personal computer’s prompt,
where it displays my user name (i.e. pouria) followed by a
tilde (~). A terminal prompt may be different in each computer and
operating system.
Here is how we implement the input() function:
input('Please enter your name: ')which is exactly the same as:
input(prompt='Please enter your name: ')If we save one of the above in a notebook and execute it, we will see:
python3 script_b.py
Please enter your name: _
The terminal cursor, displayed as an underscore in our example, will be
in front of the prompt (i.e. 'Please enter your name: ')
waiting for a response. Once it receives a response, it will proceed to
run the rest of the code (if any), or terminate the execution.
We may store the user’s response in a variable. Variables are the topic of the next section, where we shall also review more examples on input() and how we can use it to produce results based on the responses we receive from the user.
Remember
Python is an interpreted language; that is, the code we write is executed by the Python interpreter one line at a time. The input() function performs a blocking process. This means that the execution of the code by the Python interpreter is halted upon encountering an input() function until the user enters a value. Once a value is entered, the interpreter then proceeds to execute the next line.
input('Please enter the name of a protein: ')Variables And Types
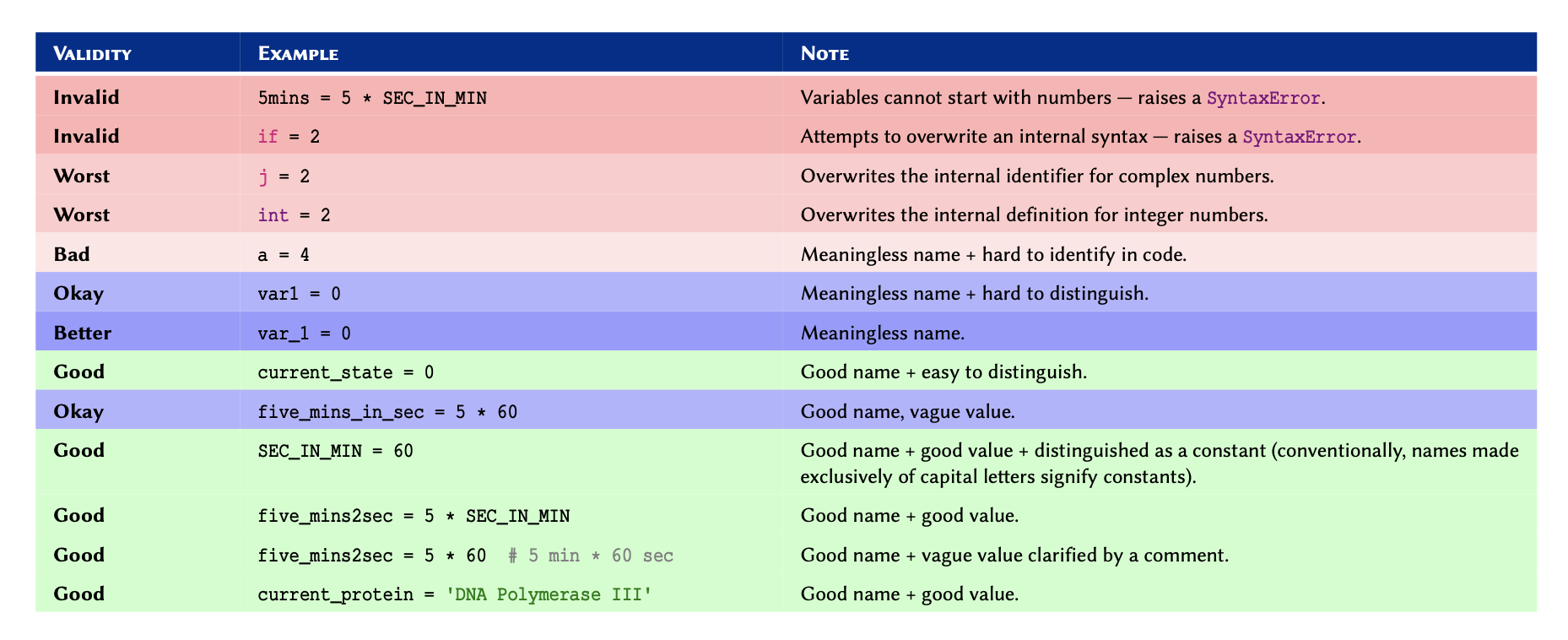
We use variables to store data in the memory. Each variable has 3 characteristics: scope, name, and type. Scope and name must be mutually unique. Starting with name, we will discuss each of these characteristics in more details throughout this chapter.
Variable names
Name of a variable is in fact an alias for a location in the memory. You
can think of it as a postbox, which is used as a substitute for an
address. Similarly, we use variable names so we wouldn’t have to use the
actual address to the location we want in the memory because it would
look something like 0x106fb8348.
There are some relatively simple rules to follow when defining variable names, which ultimately boil down to:
Remember
We should never overwrite an existing, built-in definition or identifier
(e.g. int or print). We will be learning many
such definitions and identifiers as we progress through this course.
Nonetheless, the Jupyterlab notebook as well as any good IDE highlights
syntaxes and built-in identifiers in different colours. In JupyterLab
the default for built-in definitions is green. The exact colouring
scheme depends on the IDE and the theme.
Once a variable is defined, its value may be altered or reset:
OUTPUT
2Variables containing integer numbers are known as int,
and those containing decimal numbers are known as float in
Python.
OUTPUT
3OUTPUT
3.2OUTPUT
16.0
Variables can contain characters as well; but to prevent Python from
confusing them with meaningful commands, we use quotation marks. So long
as we remain consistent, it doesn’t matter whether we use single or
double quotations. These variables are known as string or
str:
OUTPUT
Hi, John DoeDo it Yourself
Oxidised low-density lipoprotein (LDL) receptor 1 mediates the recognition, internalisation and degradation of oxidatively modified low density lipoprotein by vascular endothelial cells. Using the Universal Protein Resource (UniProt) website, find this protein for humans, and identify:
- UniProt entry number.
- Length of the protein (right at the top).
- Gene name (right at the top).
Store the information you retrieved, including the protein name, in 4 separate variables.
Display the values of these 4 variables in one line, and separate the items with 3 spaces, as follows:
Name EntryNo GeneName Length
Do it Yourself
Write a script that upon execution, asks the user to enter the name of an enzyme and then retains the response in an appropriately named variable.
Use the variable to display an output similar to the following:
ENZYME_NAME is an enzyme.
where ENZYME_NAME is the name of the enzyme entered in
the prompt.
Now alter your script to ask the user to enter the number of amino acids in that enzyme. Retain the value in another appropriately named variable.
Alter the output of your script to display a report in the following format:
ENZYME_NAME is an enzyme containing a total number of AMINO_ACIDS} amino acids.
where AMINO_ACIDS is the number of amino acids.
enzyme = input('Please enter the name of an enzyme: ')
print(enzyme, 'is an enzyme.')
length = input('How many amino acids does the enzyme contain? ')
print(enzyme, 'is an enzyme containing a total number of', length, 'amino acids.')Variable Types
When it comes to types, programming languages may be divided into two distinct categories:
Advanced Topic
In computer programming, type systems are syntactic methods to enforce and / or identify levels of abstraction. An entire field in computer science has been dedicated to the study of programming languages from a type–theoretic approach. This is primarily due to the implication of types and their underlying principles in such areas in software engineering as optimisation and security. To learn more about the study of type systems, refer to: Pierce B. Types and programming languages. Cambridge, Mass.: MIT Press; 2002.
Why learn about types in a dynamically typed programming language?
Python enjoys a powerful type system out of the box. Table Built-in types in Python provides a comprehensive reference for the built-in types in Python. Built-in types are the types that exist in the language and do not require any third party libraries to implement or use.
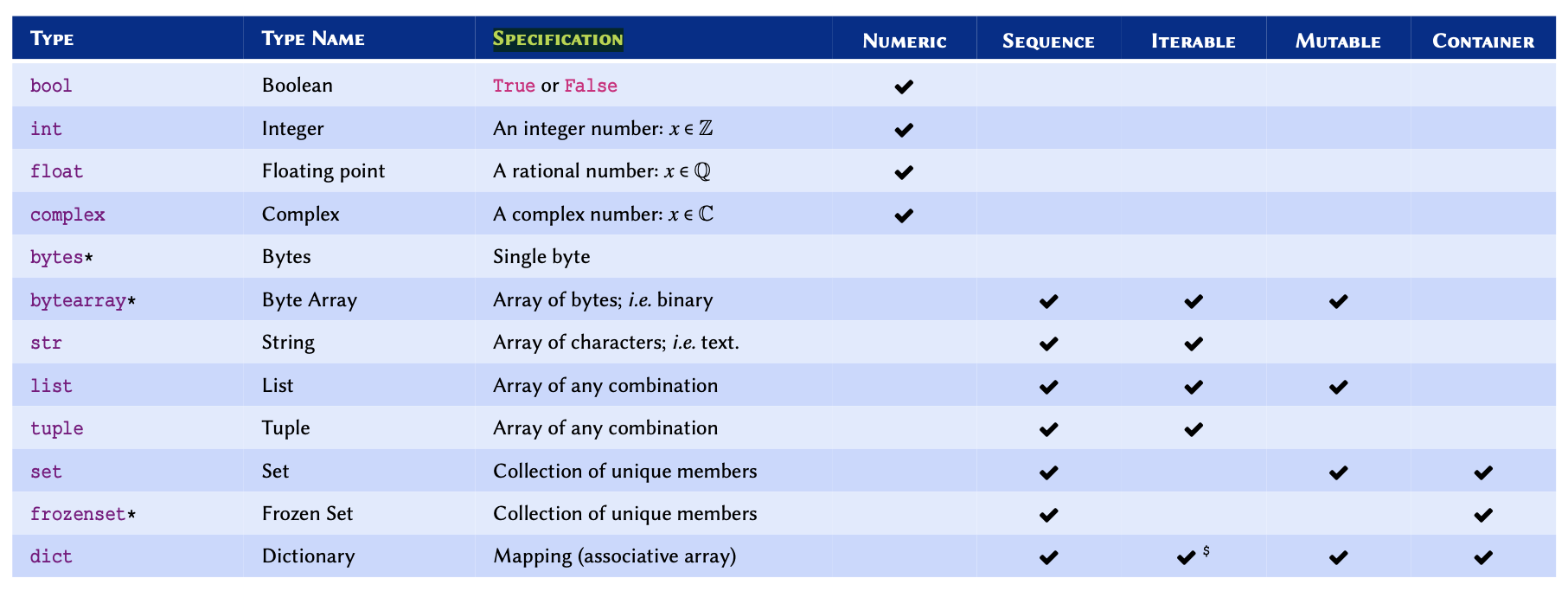
* Not discussed in this course — included for reference only.
$
dict is not an iterable by default, however, it is possible
to iterate through its keys. Mutability is an important concept in programming. A mutable object is an object whose value(s) may be altered. This will become clearer once we study
list and
tuple. Find out more about mutability in Python from the documentations}.
Complex numbers refer to a set of numbers that have a real part, and an imaginary part; where the imaginary part is defined as \(\sqrt{-1}\). These numbers are very useful in the study of oscillatory behaviours and flow (e.g. heat, fluid, electricity). To learn more about complex numbers, watch this Khan Academy video tutorial.
Sometimes we might need want to know what is the type of a variable. To do so, we use the build-in function type() as follows:
OUTPUT
<class 'int'>OUTPUT
<class 'float'>OUTPUT
<class 'float'>OUTPUT
<class 'complex'>OUTPUT
<class 'str'>OUTPUT
Value 32 is an instance of <class 'int'>PYTHON
value = 24.3454
value_type = type(value)
print('Value', value, 'is an instance of', value_type)OUTPUT
Value 24.3454 is an instance of <class 'float'>PYTHON
value = 2.5 + 1.5
value_type = type(value)
print('Value', value, 'is an instance of', value_type)OUTPUT
Value 4.0 is an instance of <class 'float'>PYTHON
value = "RNA Polymerase III"
value_type = type(value)
print('Value', value, 'is an instance of', value_type)OUTPUT
Value RNA Polymerase III is an instance of <class 'str'>OUTPUT
Value 0 is an instance of <class 'int'>PYTHON
value = .5 - 1
value_type = type(value)
print('Value', value, 'is an instance of', value_type)OUTPUT
Value -0.5 is an instance of <class 'float'>PYTHON
value = 1.3e-5
value_type = type(value)
print('Value', value, 'is an instance of', value_type)OUTPUT
Value 1.3e-05 is an instance of <class 'float'>OUTPUT
Value 300000.0 is an instance of <class 'float'>Conversion of types
Why convert types?
It is sometimes necessary to have the values returned by the input() function — i.e. the user’s response, in other types. Imagine the following scenario:
“We ask our user to enter the
total volume of their purified protein, so that we can work out the
amount of assay they need to conduct a specific experiment. To calculate
this assay volume using the volume of the purified protein, we need to
perform mathematical calculations based on the response we receive from
our user. It is not possible to perform mathematical operations on
non-numeric values. Therefore, we ought to somehow convert the type from
str to a numeric type.”
The possibility of converting from one type to another depends entirely
on the value, the source type, and the target
type. For instance; we can convert an instance of type
str (source type) to one of type int (target
type) if and only if the source value consists entirely of numbers and
there are no other characters.
Remember
To convert a variable from one type to another, we use the Type Name of the target type (as described in Table Built-in types in Python and treat it as a function.
For instance, to convert a variable to integer, we:
- look up the Type Name for integer from Table Built-in types in Python
- then treat the Type Name as a function:
int() - use the function to convert our variable: new_var =
int(old_var)
Here is an example of how we convert types in Python:
OUTPUT
12 <class 'str'>OUTPUT
12 <class 'int'>If we attempt to convert a variable that contains non-numeric values,
a ValueError is raised:
OUTPUT
12y <class 'str'>OUTPUT
ValueError: invalid literal for int() with base 10: '12y'Do it Yourself
In programming, we routinely face errors resulting from different mistakes. The process of finding and correcting such mistakes in the code is referred to as debugging.
We have been given the following snippet written in Python 3:
value_a = 3
value_b = '2'
result = value_a + value_b
print(value_a, '+', value_b, '=', result)but when the code is executed, we encounter an error message as follows:
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'int' and 'str'Debug the snippet so that the correct result is displayed:
3 + 2 = 5
Handling input variables
We may use type conversion in conjunction with the values returned by the input() function:
response = input('Please enter a numeric value: ')
response_numeric = float(response)
print('response:', response)
print('response type:', type(response))
print('response_numeric:', response_numeric)
print('response_numeric type:', type(response_numeric))The output shows the results when we enter numeric values as directed.
Do it Yourself
We know that each amino acid in a protein is encoded by a triplet of mRNA nucleotides.
With that in mind, alter the script you wrote for Do it Yourself and use the number of amino acids entered by the user to calculate the number of mRNA nucleotides.
Display the results in the following format:
ENZYME_NAME is an enzyme with AMINO_ACIDS amino acids and NUCLEOTIDES nucleotides.
where NUCLEOTIDES is the total number of mRNA
nucleotides that you calculated.
Note: Multiplication is represented using the
asterisk (*) sign.
enzyme = input('Please enter the name of an enzyme: ')
length = input('How many amino acids does the enzyme contain? ')
nucleotides = 3 * int(length)
print(enzyme, 'is an enzyme with', length, 'amino acids and', nucleotides, 'nucleotides.')Variable scopes
Resolution of namesWhen defining a variable, we should always consider where in our programme we intent to use it. The more localised our variables, the better. This is because local variables are easier to distinguish, and thus reduce the chance of making mistakes — e.g. unintentionally redefine or alter the value of an existing variable.
To that end, the scope of a variable defines the ability to reference a variable from different points in our programmes. The concept of local variables becomes clearer once we explore functions in programming in chapter Functions.
As displayed in Figure Variable scopes, the point at or from which a variable can be referenced depends on the location where the variable is defined.
In essence, there are three general rules to remember in relation variable scopes in Python:
I. A variable that is defined in the outer scope, can be accessed or called in the inner scopes, but it cannot be altered implicitly. Not that such variables may still be altered using special techniques (not discussed).
- A variable that is defined in the innermost scopes (local), can only be accessed, called, or altered within the boundaries of the scope it is defined in.
- The inner scopes from which a variable is referenced must
themselves have be contained within the defining scope — e.g. in
FuncBof Figure Variable scopes, we can referencea,b, andx; but notf1. This is because the scope off1isScript→FuncA, so it can only be referenced fromScript→FuncA→ …, but not `Script→ … orScript→FuncB→ ….

Python is an interpreted language. This means that the Python
interpreter goes through the codes that we write line by line,
interpreting it to machine language. It is only then that the commands
are processed and executed by the computer. On that account, a variable
(or a function) can be referenced only after its initial
definition. That is why, for instance, in Script (part 2)
of Figure Variable scopes, we can
reference every variable and function except for FuncC,
which is declared further down the code hierarchy.
Although scope and hierarchy appear at first glance as theoretical concepts in programming, their implications are entirely practical. The definition of these principles vary from one programming language to another. As such, it is essential to understand these principles and their implications in relation to any programming language we are trying to learn.
Operations
Through our experimentations with variable types, we already know that variables may be subject to different operations.
When assessing type conversions we also established that the operations we can apply to each variable depend on the type of that variable. To that end, we learned that although it is sometimes possible to mix variables from different types to perform an operation — e.g. multiplying a floating point number with an integer, there are some logical restrictions in place.
Throughout this section, we will take a closer look into different types of operations in Python. This will allow us to gain a deeper insight into the concept and familiarise ourselves with the underlying logic.
To recapitulate on what we have done so far, we start off by reviewing additions — the most basic of all operations.
Give the variable total_items:
OUTPUT
2We can increment the value of an existing variable by
1 as follows:
OUTPUT
3Given 2 different variables, each containing a different value; we can perform an operation on these values and store the result in another variable without altering the original variables in any way:
OUTPUT
7We can change the value of an existing variable using the value stored in another variable:
OUTPUT
12There is also a shorthand method for applying the operation on an existing variable:
OUTPUT
2OUTPUT
3OUTPUT
8As highlighted in the introduction, different operations may be applied to any variable or value. Throughout the rest of this section, we will explore the most fundamental operations in programming, and learn about their implementation in Python.
Mathematical Operations
Suppose a and b are 2 variables
representing integer numbers as follows:
a = 17
b = 5Using a and b we can itemise built-in
mathematical operations in Python as follows:

Remember
As far as mathematical operations are concerned, variables
a and b may be an instance of any
numeric type. See Table Routine
mathematical operations in Python to find out more about numeric
types in Python.
Values of type int have been chosen in our examples to
facilitate the understanding of the results.
Do it Yourself
- Calculate the following and store the results in appropriately named variables:
- \(5.8 \times 3.3\)
- \(\frac{180}{6}\)
- \(35 - 3.0\)
- \(35 - 3\)
- \(2^{1000}\)
Display the result of each calculation – including the type, in the following format:
Result: X is an instance of <class 'Y'>
- Now using the results you obtained:
I. Can you explain why is the result of \(35 - 3.0\) is an instance of type
float, whilst that of \(35 - 3\) is of typeint?
II. Unlike the numeric types, string values have a
length. To obtain the length of a string value, we use len().
Convert the result for \(2^{1000}\)
from int to str, then use the aforementioned
function to work out the length of the number — i.e. how many digits is
it made of?
If you feel adventurous, you can try this for \(2^{10000}\) or higher; but beware that you might overwhelm your computer and need a restart it if you go too far (i.e. above \(2^{1000000}\)). Just make sure you save everything beforehand, so you don’t accidentally step on your own foot.}
Hint: We discuss len() in subsection of arrays. However, at this point, you should be able to use the official documentations and StackOverflow to work out how it works.
OUTPUT
Result: 19.139999999999997 is an instance of <class 'float'>OUTPUT
Result: 30.0 is an instance of <class 'float'>OUTPUT
Result: 32.0 is an instance of <class 'float'>OUTPUT
Result: 32 is an instance of <class 'int'>OUTPUT
Result: 10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376 is an instance of <class 'int'>
In the case of \(35 - 3.0\) vs \(35 - 3\), the former includes a floating
point number. Operations involving multiple numeric types always produce
the results as an instance of the type that covers all of the operands –
i.e. float covers int, but not vice-versa.
Shorthands
When it comes to mathematical operations in Python, there is a frequently used shorthand method that every Python programmer should be familiar with.
Suppose we have a variable defined as total_residues = 52
and want to perform a mathematical operation on it. However, we would
like to store the result of that operation in
total_residues instead of a new variable. In such cases, we
can do as follows:
OUTPUT
60OUTPUT
50OUTPUT
100OUTPUT
25.0OUTPUT
12.0OUTPUT
2.0OUTPUT
8.0We can also perform such operations using multiple variables:
PYTHON
total_residues = 52
new_residues = 8
number_of_proteins = 3
total_residues += new_residues
print(total_residues)OUTPUT
60OUTPUT
84Do it Yourself
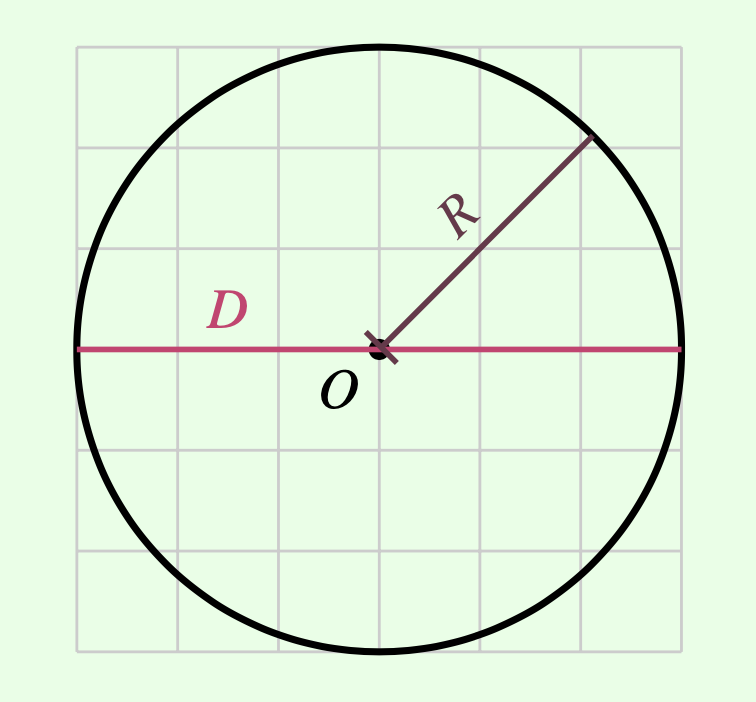
- Given:
- Circumference: \(C = 18.84956\)
- Radius: \(R = 3\)
and considering that the properties of a circle are defined as follows:
\[\pi = \frac{C}{D}\] calculate
\(\pi\) using the above equation and
store it in a variable named pi:
Then round the results to 5 decimal places and display the result in the following format:
The value of pi calculated to 5 decimal places: X.XXXXX
Note: To round floating point numbers in Python, we use round(). This is a built-in function that takes 2 input arguments: the first is the variable/value to be rounded, and the second is the number decimal places. Read more about round() in the official documentations.
-
Now without creating a new variable, perform the following operation:
\[pi = \frac{pi}{(3 \bmod 2) - 1}\]
where the expression ’‘\(3 \bmod 2\)’’ represents the remainder for the division of 3 by 2.
Explain the output.
pi /= (3 % 2) - 1
The calculation raises a ZeroDivisionError. This is
because division by zero is mathematically impossible.
Precedence
In mathematics and computer programming, there is a collection of conventional rules on the precedence of procedures to evaluate a mathematical expression. This collection of rules is referred to as the order of operation or operator precedence.
Suppose we have a mathematical expression as follows:
\[x = 2 + 3 \times 9\]Such an expression can only be evaluated correctly if we do the multiplication first and then perform the addition. This means that the evaluation is done as follows:
\[given:3 \times 9 = 27\] \[\implies x = 2 + 27\] \[ = 29\]
For instance, in an expression such as:
\[x = 2 \times (3 + (5 - 1)^2)\]
the evaluation workflow may be described as follows:
\[x = 2 \times (3 + 4^2)\] \[ = 2 \times (3 + 16)\] \[ = 38\]The same principle applies in Python. This means that if we use Python to evaluate the above expression, the result would be identical:
OUTPUT
38Do it Yourself
Display the result of each item in the following format:
EXPRESSION = RESULTFor example:
2 + 3 = 5- Calculate each expression without using parentheses:
- \(3 \times \frac{2}{4}\)
- \(5 + 3 \times \frac{2}{4}\)
- \(3 \times \frac{2}{4} + 5\)
- \(\frac{2}{4} \times 3\)
- Calculate these expressions using parentheses:
- \(5 + \frac{2}{4} \times 3\)
- \(5 + \frac{2 \times 3}{4}\)
- \(5 + \frac{2}{4 \times 3}\)
- Given
a = 2
b = 5use a and b to calculate the following
expressions:
- \((a + b)^2\)
- \(a^2 + 2ab + b^2\)
OUTPUT
3 * 2 / 4 = 1.5OUTPUT
5 + 3 * 2 / 4 = 6.5OUTPUT
3 * 2 / 4 + 5 = 6.5OUTPUT
2 / 4 * 3 = 1.5Non-numeric values
It sometimes makes sense to apply some mathematical operations to non-numeric variables too.
We can multiply strings to repeat them. There is no specific advantage to the use of multiplication instead of manually repeating characters or words, but it makes our code look cleaner, and that’s always a good thing!
We can also add string values to each other. This is called string concatenation. It is a useful method for concatenating a few strings and / or string variables.
PYTHON
SEPARATOR = '-' * 20
NEW_LINE = '\n'
SPACE = ' '
forename = 'Jane'
surname = 'Doe'
birthday = '01/01/1990'
full_name = forename + SPACE + surname
data = full_name + NEW_LINE + SEPARATOR + NEW_LINE + 'DoB: ' + birthday
print(data)OUTPUT
Jane Doe
--------------------
DoB: 01/01/1990Remember
New line character or '\n' is a universal directive to
induce a line-break in Unix based operating systems (MACOS) and Linux).
In WINDOWS, we usually us '\r' or '\r\n'
instead. These are known as escape sequences,
which we explore in additional details under string operations in
chapter Strings
Do it Yourself
The risk of Huntington’s disease appears to increase proportional to the
continuous repetition of CAG nucleotides (glutamine codon)
once they exceed 35 near the beginning of the Huntingtin
(IT15) gene. The CAG repeats are also referred
to as a polyglutamine or polyQ tract.
glutamine_codon = 'CAG'- Create a polynucleotide chain representing 36 glutamine codons.
Store the result in a variable called
polyq_codons.
Display the result as:
Polyglutamine codons with 36 repeats: XXXXXXXXX...- Use len() to work out the length of
polyq_codons, and store the result in a variable calledpolyq_codons_length.
Display the result in the following format:
Number of nucleotides in a polyglutamine with 36 repeats: XXXUse len() to work out the length of
glutamin_codon, and store the result in variableamino_acids_per_codon.Divide
polyq_codons_lengthbyamino_acids_per_codonto prove that the chain contains the codon for exactly 36 amino acids. Store the result in variablepolyq_peptide_length.
Display the result in the following format:
Number of amino acids in a polyglutamine with 36 repeats: XXX- Determine the types for the following variable:
amino_acids_per_codon
polyq_codons_length
-
polyq_peptide_length
and display the result for each item in the following format:
Value: XXX - Type: <class 'XXXX'>Are all the variables in task #5 of the same type? Why?
Repeat from task #4, but this time use an alternative method of division as outlined in See Table Routine mathematical operations in Python.
PYTHON
print('Value:', amino_acids_per_codon, '- Type:', type(amino_acids_per_codon))
print('Value:', polyq_codons_length, '- Type:', type(polyq_codons_length))
print('Value:', polyq_peptide_length, '- Type:', type(polyq_peptide_length))OUTPUT
Value: 3 - Type: <class 'int'>
Value: 108 - Type: <class 'int'>
Value: 36.0 - Type: <class 'float'>
No, polyq_peptide_length is an instance of type
float. This is because we used the normal division
(/) and not floor division (//}) to calculate
its value. The result of normal division is always presented as a
floating point number.
PYTHON
polyq_peptide_length = polyq_codons_length // amino_acids_per_codon
print('Number of amino acids in a polyglutamine with 36 repeats:', polyq_peptide_length)
print('Value:', amino_acids_per_codon, '- Type:', type(amino_acids_per_codon))
print('Value:', polyq_codons_length, '- Type:', type(polyq_codons_length))
print('Value:', polyq_peptide_length, '- Type:', type(polyq_peptide_length))OUTPUT
Number of amino acids in a polyglutamine with 36 repeats: 36
Value: 3 - Type: <class 'int'>
Value: 108 - Type: <class 'int'>
Value: 36 - Type: <class 'int'>Logical Operations
An operation may involve a comparison. The result of such operations is
either True or False. This is known as the
Boolean or bool data type. In reality, however,
computers record True and False as
1 and 0 respectively.
Operations with Boolean results are referred to as logical operations. Testing the results of such operations is known as truth value testing.
Given the two variables a and b as
follows:
a = 17
b = 5Boolean operations may be defined as outlined in Table Routine logical operations in Python..

Do it Yourself
We know that in algebra, the first identity (square of a binomial) is:
\[(a + b)^2 = a^2 + 2ab + b^2\] now given:
a = 15
b = 4- Calculate
\[y_1 = (a + b)^{2}\] \[y_2 = a^2 + 2ab + b^2\]
Display the results in the following format:
y1 = XX
y2 = XX
- Determine whether or not
y_1is indeed equal toy_2. Store the result of your test in another variable calledequivalence. Display the results in the following format:
Where a = XX and b = XX:
y1 is equal to y2: [True/False]Negation
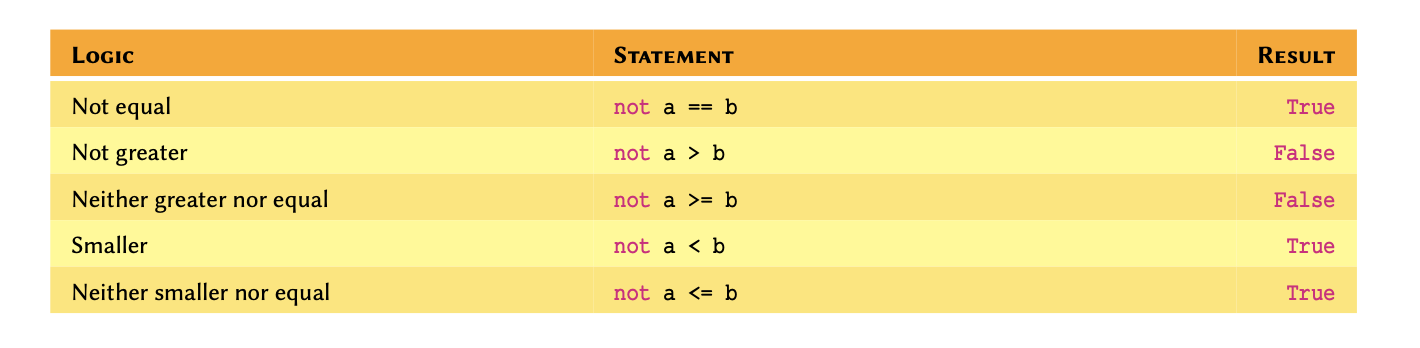
We can also use negation in logical operations. Negation in Python is implemented using not:
Do it Yourself
Using the information from previous Do it Yourself:
- Without using not, determine whether or not
y_1is not equal toy_2. Display the result of your test and store it in another variable calledinequivalent.
- Negate
inequivalentand display the result.
Disjunctions and Conjunctions
Logical operations may be combined using conjunction with and and disjunction with or to create more complex logics:

Do it Yourself
Given
a = True
b = False
c = TrueEvaluate the following statements:
- a == b
- a == c
- a
orb - a
andb - a
orbandc - (a
orb)andc -
notaor(bandc) -
notaornot(bandc) -
notaandnot(bandc) -
notaandnot(borc)
Display the results in the following format:
1. [True/False]
2. [True/False]
...Given that:
Complex logical operations
It may help to break down more complex operations, or use parenthesis to make them easier to both read and write:

Notice that in the last example, all notations are essentially the same and only vary in terms of their collective results as defined using parenthesis. Always remember that in a logical statement:
OUTPUT
TrueOUTPUT
TrueOUTPUT
TrueOUTPUT
FalseOUTPUT
TrueOUTPUT
FalseOUTPUT
TruePYTHON
# Disjunction and negated conjunction and conjunction:
# true AND NOT false AND false
a < b or not b < c and b > aOUTPUT
FalsePYTHON
# Disjunction and negated conjunction - similar to the
# previous example: true AND NOT (false AND false)
a < b or not (b < c and b > a)OUTPUT
TrueThese are only a few examples. There are endless possibilities, try them yourself and see how they work.
To that end, you may want to use variables to split complex statements down to smaller portions:
PYTHON
age_a, age_b = 15, 35
are_positive = age_a > 0 and age_b > 0
a_is_older = are_positive and (age_a > age_b)
b_is_older = are_positive and (age_a < age_b)
a_is_teenager = are_positive and 12 < age_a < 20
b_is_teenager = are_positive and 12 < age_b < 20
a_is_teenager and b_is_olderOUTPUT
TrueOUTPUT
FalseOUTPUT
TrueDo it Yourself
Given
a = 3
b = 13Test the following statements and display the results:
- \(a^2 < b\)
- \(3 - a^3 < b\)
- \(|25 - a^2| > b\)
- \(25 \bmod a^2 > b\)
- \(25 \bmod a^2 > b\) or \(25 \bmod b < a\)
- \(25 \bmod a^2 < b\) and \(25 \bmod b > a\)
- \(\frac{12}{a}\) and \(a\times4 < b\)
where “|…|” represents the absolute value, and “\(n \bmod m\)” represents the remainder for the division of \(n\) by \(m\).}
Display the results in the following format:
1. [True/False]
2. [True/False]
...Exercises
End of chapter Exercises
Write and execute a Python script to display your own name as an output in the terminal.
Write and execute a Python script that:
- Displays the text
Please press enter to continue..., and waits for the user to press enter. - Once the user pressed enter, the program should display
Welcome to my programme!before it terminates.
-
We have an enzyme whose reaction velocity is \(v=50~mol \cdot L^{-1} \cdot s^{-1}\) at the substrate concentration of \([S] = K_{m} = 2.5~mol \cdot L^{-1}\). Work out the maximum reaction velocity or \(V_{\max}\) for this enzyme using the Michaelis-Menten equation:
\[v = \frac{V_{\max} [\textrm{S}]}{K_{m} + [\textrm{S}]}\]
Key Points
- Two key functions for I/O operations are print() and input()
- Three most commonly used variables such as
int,float, andstr. - Variable scope can be local or global depending where they are being used.
- Mathematical operations follow conventional rules of precedence
- Logical operations provide results in Boolean (True or False)