Functions
Last updated on 2024-05-23 | Edit this page
Download Chapter notebook (ipynb)
Overview
Questions
- What are functions?
- How are functions created?
- What are optional arguments?
- What makes functions powerful?
Objectives
- Develop concepts of using functions.
- Understanding different ways of creating functions.
- Explaining input arguments.
- Understanding the inter-connectivity of functions.
This chapter assumes that you are familiar with the following concepts in Python 3:
Functions
In programming, functions are containers that incorporate some code and perform very specific tasks. As we learned in the first chapter (on outputs), a function usually takes in one or several variables or values, processes them, and produces a specific result. The variable(s) given to a function and those produced by it are referred to as input arguments, and outputs respectively.
There are different ways to create functions in Python. In this course, we will be using def to implement our functions. This is the easiest and by far the most common method for declaring functions. The structure of a typical function defined using def is as follows:
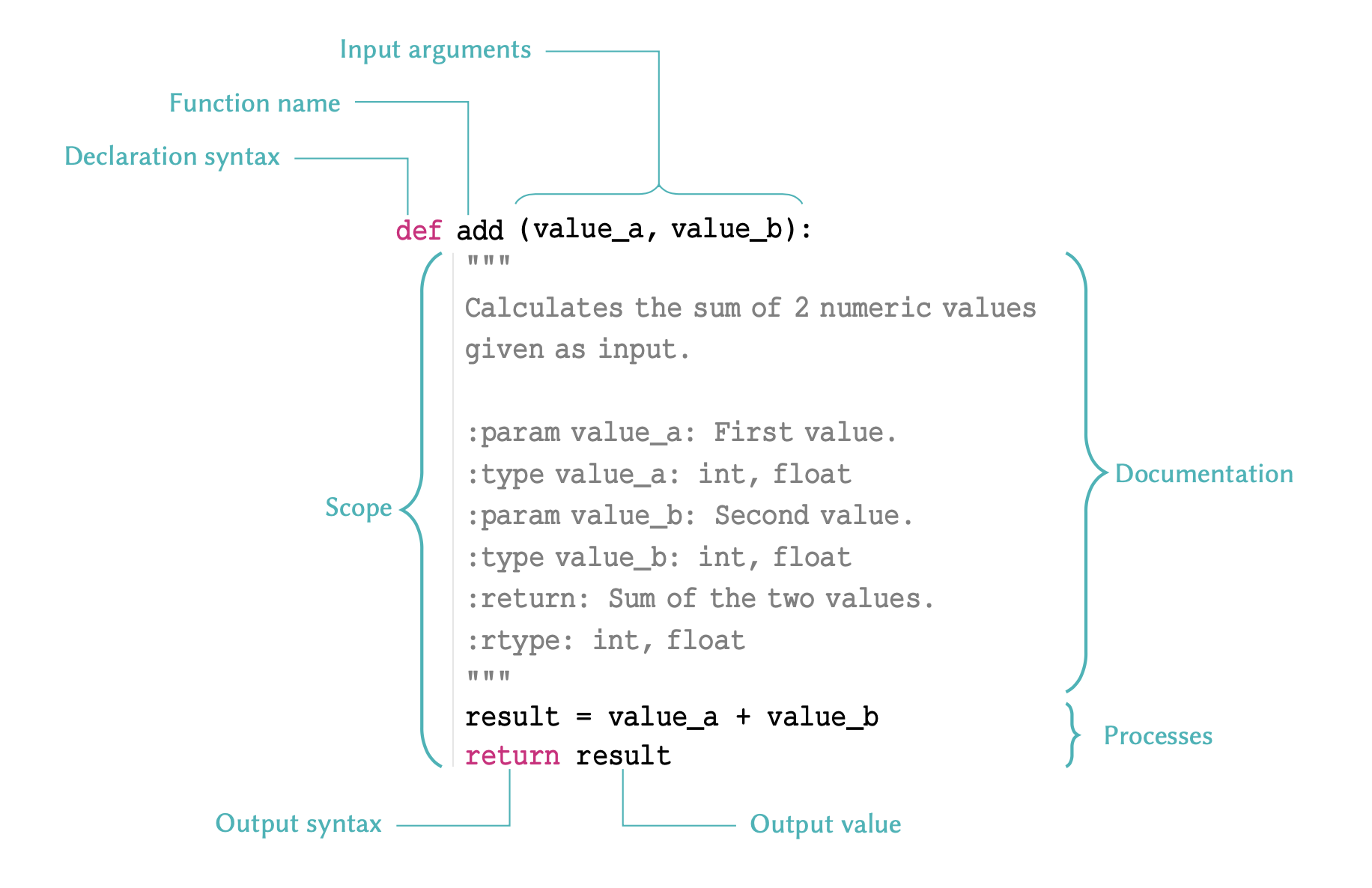
Remember
There are several points to remember in relation to functions:
- The name of a function follows same principles as that of any other variable as discussed in variable names. The name must be in lower-case characters.
- The input arguments of a function — e.g. value_a and value_b in the above example; are essentially variables whose scope is the function. That is, they are only accessible within the function itself, and not from anywhere else in the code.
- Variables defined inside of a function, should never use the same name as variables defined outside of it; or they may override each other.
- A function declared using def should always be terminated with a return syntax. Any values or variables that follow return are regarded as the function’s output.
- If we do not specify a return value, or fail to terminate a function
using return altogether, the Python interpreter will
automatically terminate that function with an implicit
return None. Being an implicit process, this is generally regarded as a bad practice and should be avoided.
We implement functions to prevent repetition in our code. It is therefore important for a function to only perform a very specific task, so that it can be context-independent. You should therefore avoid incorporating separable tasks inside a single function.
Interesting Fact
Functions are designed to perform specific tasks. That is why in the majority of cases, they are named using verbs — e.g. add() or print(). We use verbs to describe an action, a state, or an occurrence in everyday language. Likewise, this type of nomenclature describes the action performed by a specific function. Name your functions wisely!
Once you start creating functions for different purposes; after a while, you will have a library of ready-to-use functions to address different needs. This is the primary principle of a popular programming paradigm known as functional programming.
So let us implement the example outline in the diagram:
PYTHON
def add(value_a, value_b):
"""
Calculates the sum of 2 numeric values
given as inputs.
:param value_a: First value.
:type value_a: int, float
:param value_b: Second value.
:type value_b: int, float
:return: Sum of the two values.
:rtype: int, float
"""
result = value_a + value_b
return resultOnce implemented, we can go ahead use the function. We can do so in the same way as we do with the built-in functions such as max() or print():
OUTPUT
7Remember
When calling a function, we should always pass our positional input arguments in the order they are defined in the function definition, from left to right.
This is because in the case of positional arguments, as the
name suggests, the Python interpreter relies on the position of
each value to identify its variable name in the function
signature. The function signature for our add function is
as follows:
add(value_a, value_b)So in the above example where we say add(2, 5), the value 2 is identified as the input argument for value_a, and not value_b. This happens automatically because in our function call, the value 2 is written in the first position, where value_a is defined in our function declaration (signature).
Alternatively, we can use the name of each input argument to pass values onto them in any order. When we use the name of the input argument explicitly, we pass the values as keyword arguments. This is particularly useful in more complex functions where there are several input arguments.
Let us now use keyword arguments to pass values to our add() function:
OUTPUT
7Now even if we changed the order of our arguments, the function would still be able to associate the values correctly:
OUTPUT
7Remember
Choose the order of your input argument wisely. This is important when your function accepts multiple input argument.
Suppose we want to define a “division” function. It makes sense to assume that the first number passed to the function will be divided by the second number:
It is also much less likely for someone to use keywords to pass arguments to this function – that is, to say:
than it is for them to use positional arguments (without any keywords), that is:
But if we use an arbitrary order, then we risk running into problems:
In which case, our function would perform perfectly well if we use keyword arguments; however, if we rely on positional arguments and common sense, then the result of the division would be calculated incorrectly.
PYTHON
result_a = divide_bad(numerator=2, denominator=4)
result_b = divide_bad(2, 4)
print(result_a == result_b)OUTPUT
FalseDo it Yourself
Implement a function called find_tata that takes in one
str argument called seq and looks for the TATA-box motif inside that
sequence. Then:
if found, the function should return the index for the TATA-box as output;
if not found, the function should explicitly return
None.
Example:
The function should behave as follows:
sequence = 'GCAGTGTATAGTC'
res = find_tata(sequence)Documentations
It is essential to write short, but proper documentation for our functions. There is no correct way document a code. However, a general rule, a good documentation should tell us:
what a function does;
the names of the input arguments, and what type each argument should be;
the output, and its type.
The documentation string, also known as the docstring, is always written inside triple quotation marks. The docstring must be the implemented on the very first line following the declaration of the function to be recognised as the documentation:
PYTHON
def add(value_a, value_b):
"""
Calculates the sum of 2 numeric values
given as inputs.
:param value_a: First value.
:type value_a: int, float
:param value_b: Second value.
:type value_b: int, float
:return: Sum of the two values.
:rtype: int, float
"""
result = value_a + value_b
return resultRemember
You might feel as though you would remember what your own functions do. That, however, is scarcely the case. Functions that we implement tend to perform specialist, and at times, very complex and interconnected processes. Whilst you might remember what a specific function does for a few days after writing it, you would almost certainly have trouble remembering the details in a matter of months. And that is not even considering details regarding the type of the input argument(s) and those of the output. In addition, programmers often share their works with other fellow programmers; be it with their team, or in the context of a publication, or in public repositories as a contribution to the community. Whatever the reason, there is one golden rule: a functionality does not exist unless it is documented.
Writing the docstring on the first line is important because once a function is documented; we can use help(), which is a built-in function, to access the documentations as follows:
OUTPUT
Help on function add in module __main__:
add(value_a, value_b)
Calculates the sum of 2 numeric values
given as inputs.
:param value_a: First value.
:type value_a: int, float
:param value_b: Second value.
:type value_b: int, float
:return: Sum of the two values.
:rtype: int, floatFor very simple functions – e.g. the function add() that we implemented above, where it is fairly obvious what are the input and output arguments and their respective types; it is okay to simplify the docstring to something explicit and concise, such as follows:
PYTHON
def add(value_a, value_b):
"""value_a + value_b -> number"""
result = value_a + value_b
return resultOUTPUT
Help on function add in module __main__:
add(value_a, value_b)
value_a + value_b -> numberDo it Yourself
Re-implement the function you defined in the previous Do it Yourself with appropriate documentations.
Optional arguments
We already know that most functions take in one or more input arguments. Sometime a function does not need all of the arguments to perform a specific task.
An example we have already worked with is print(). We already
know that this function may be utilised to display text on the screen.
However, we also know that if we use the file argument, it
will behave differently in that it will write the text inside a file
instead of displaying it on the screen. Additionally, print()
has other arguments such as sep or end, which
have specific default values of ’
’ (a single space) and \n (a linebreak) respectively.
Remember
Input arguments that are necessary to call a specific function are referred to as non-default arguments. Those whose definition is not mandatory for a function to be called are known as default or optional arguments.
Optional arguments may only be defined after
non-default arguments (if any). If this order is not respected, a
SyntaxError will be raised.
Advanced Topic
The default value defined for optional arguments can in theory be an instance of any type in Python. However, it is better and safer to only use immutable types as demonstrated in Table for default values. The rationale behind this principle is beyond the scope of this course, but you can read more about it in the official documentations.
To define functions with optional arguments, we need to assign to them a default value. Remember that input arguments are variables with a specific scope. As a result, we can treat our input argument as variables and assign them a value:
PYTHON
def prepare_seq(seq, name, upper=False):
"""
Prepares a sequence to be displayed.
:param seq: Sequence
:type seq: str
:param name: Name of the sequence.
:type name: str
:param upper: Convert sequence to uppercase characters (default: False)
:type upper: bool
:return: Formated string containing the sequence.
:rtype: str
"""
template = 'The sequence of {} is: {}'
if not upper:
response = template.format(name, seq)
else:
seq_upper = seq.upper()
response = template.format(name, seq_upper)
return responseNow if we don’t explicitly define upper when calling
prepare_seq(), its value is automatically considered to be
False:
OUTPUT
The sequence of DNA is: TagCtGCIf we change the default value of False for
upper and set to True, our sequence should be
converted to upper case characters:
OUTPUT
The sequence of DNA is: TAGCTGCDo it Yourself
Modify the function from previous Do it Yourself to accept an
optional argument called upper, with default value
of False; thereafter:
if
upperisFalse, then the function should perform as it already does (similar to previous Do it Yourself);if
upperisTrue, then the function should convert the sequence onto uppercase characters before it looks for the TATA-box.
Do not forget to update the docstring of your function.
PYTHON
def find_tata(seq, upper=False):
"""
Finds the location of the TATA-box,
if one exists, in a polynucleotide
sequence.
:param seq: Polynucleotide sequence.
:type seq: str
:param upper: Whether or not to
homogenise the sequence
to upper-case characters.
:type upper: bool
:return: Start of the TATA-box.
:rtype: int
"""
tata_box = 'TATA'
if not upper:
result = seq.find(tata_box)
else:
seq_prepped = seq.upper()
result = seq_prepped.find(tata_box)
return resultIt is possible to have more than one return in a function. This is useful when we need to account for different outcomes; such as the one we saw in the previous example with prepare_seq().
This means that we can simplify the process as follows:
PYTHON
def prepare_seq(seq, name, upper=False):
"""
Prepares a sequence to be displayed.
:param seq: Sequence
:type seq: str
:param name: Name of the sequence.
:type name: str
:param upper: Convert sequence to uppercase characters (default: False)
:type upper: bool
:return: Formated string containing the sequence.
:rtype: str
"""
template = 'The sequence of {} is: {}'
if not upper:
return template.format(name, seq)
seq_upper = seq.upper()
return template.format(name, seq_upper)Notice that we got rid of response. Here is a description of what happens:
In this context, if the conditional statement holds — i.e. when
upperisFalse, we enter the if block. In that case, we reach the firstreturnstatement. At this point, the function returns the corresponding results and terminates immediately.On the other hand, if the condition does not hold — i.e. where
upperisTrue, we skip the if block altogether and proceed. It is only then that we arrive at the secondreturnstatement where the alternative set of results are prepared.
This does not alter the functionality of our function in any way. However, in complex functions that may be called repetitively (e.g. inside for loop), this technique may improve the performance of the function.
Now if we call our function, it will behave in exactly the same way as it did before:
OUTPUT
The sequence of DNA is: TagCtGCOUTPUT
The sequence of DNA is: TAGCTGCInterconnectivity of functions
Functions can call other functions. This is what makes them extremely powerful tools that may be utilised to address an unlimited number of problems.
This allows us to devise a network of functions that call each other to perform different tasks at different times, and collectively contribute to the production of one final answer.
Remember
Functions must have specialist functionalities. They should, as much as possible, be implemented to perform one task, and one task only.
So if you need to get more things done, do not write more code in one function. This would defy the purpose of functional programming. Instead, consider writing more functions that contain less code and perform more specialist functionalities.
EXAMPLE: A mini toolbox for statistics

PYTHON
def mean(arr):
"""
Calculates the mean of an array.
:param arr: Array of numbers.
:type arr: list, tuple, set
:return: Mean of the values in the array.
:rtype: float
"""
summation = sum(arr)
length = len(arr)
result = summation / length
return resultNow that we have function to calculate the mean, we can go ahead and write a function to calculate the variance, which itself relies on mean:
PYTHON
def variance(arr):
"""
Calculates the variance of an array.
:param arr: Array of numbers.
:type arr: list, tuple, set
:return: Variance of the values in the array.
:rtype: float
"""
arr_mean = mean(arr)
denominator = len(arr)
numerator = 0
for num in arr:
numerator += (num - arr_mean) ** 2
result = numerator / denominator
return resultNow we have two functions, which we can use to calculate the variance or the mean for any array of numbers.
Remember that testing a function a crucial part of its design. So let us go ahead and test our functions:
OUTPUT
134.58871428571427OUTPUT
109633.35462420408Now that we have a function to calculate the variance, we could easily go on to calculate the standard deviation, too.
The standard deviation is calculated from the square root of variance. We can easily implement this in a new function as follows:
PYTHON
def stan_dev(arr):
"""
Calculates the standard deviation of an array.
:param arr: Array of numbers.
:type arr: list, tuple, set
:return: Standard deviation of the values in the array.
:rtype: float
"""
from math import sqrt
var = variance(arr)
result = sqrt(var)
return resultNow let’s see how it works in practice:
OUTPUT
331.1092789762982Do it Yourself
Write a function that given an array of any values, produces a dictionary containing the value of that array as keys, and the count of the values in the original array (their frequencies) as values.
Example:
For the following array:
the function should return the above dictionary:
Suggestion: You can add this as a new tool to the statistics mini toolbox.
PYTHON
def count_values(arr):
"""
Converts an array into a dictionary of
the unique members (as keys) and their
counts (as values).
:param arr: Array containing repeated
members.
:type arr: list, tuple
:return: Dictionary of unique members
with counts.
:rtype: dict
"""
unique = set(arr)
arr_list = list(arr)
result = dict()
for num in unique:
result[num] = arr_list.count(num)
return resultExercises
End of chapter Exercises
Write a function with the following features:
Call the function get_basic_stats() and let it take one input argument which, however, may contain any number of input arrays, e.g. a tuple of arrays.
Using a for loop, for each of the arrays calculate the mean and the variance using the functions ‘mean’ and ‘variance’ given above, i.e. call those functions from within the function get_basic_stats().
Calculate the standard deviation for each array as the square root of the variance. You will have to import the function
sqrtfrom modulemath.Return a single array containing (in that order) the mean, the variance, and the standard deviation for each array.
To test the function, combine three arrays in a tuple as follows:
Call the function get_basic_stats() with this tuple as argument and write the output to a variable. Display the results in the following form:
STD of array' index, ':' STDThe result for the above arrays should be:
STD of array 0 : 1.4142135623730951
STD of array 1 : 0.0
STD of array 2 : 0.14357537702854514PYTHON
def mean(arr):
"""
Calculates the mean of an array.
:param arr: Array of numbers.
:type arr: list, tuple, set
:return: Mean of the values in the array. :rtype: float
"""
summation = sum(arr)
length = len(arr)
result = summation / length
return result
def variance(arr):
"""
Calculates the variance of an array.
:param arr: Array of numbers.
:type arr: list, tuple, set
:return: Variance of the values in the array.
:rtype: float
"""
arr_mean = mean(arr)
denominator = len(arr)
numerator = 0
for num in arr:
numerator += (num - arr_mean) ** 2
result = numerator / denominator
return result
def get_basic_stats(arrays):
"""
Calculates the mean, variance and standard deviation for
a set of arrays.
:param arrays: An array contain any number of arrays of numbers.
:type arrays: list, tuple
:return: A list of arrays containing the mean, variance and
standard deviation for each item in arrays
:rtype: list
"""
from math import sqrt
results = list()
for array in arrays:
arr_mean = mean(array)
arr_var = variance(array)
arr_std = sqrt(arr_var)
results.append((arr_mean, arr_var, arr_std))
return results
my_arrays = ([1, 2, 3, 4, 5],
[7, 7, 7, 7],
[1.0, 0.9, 1.2, 1.12, 0.95, 0.76],
)
my_results = get_basic_stats(my_arrays)
for index, result in enumerate(my_results):
print('STD of array', index, ': ', result[2])OUTPUT
STD of array 0 : 1.4142135623730951
STD of array 1 : 0.0
STD of array 2 : 0.14357537702854514